Modelle

Diskussionspunkte im Zusammenhang mit Modellen
  • Was ist ein Modell?
  • Wie gelangt man von einem realen Phänomen zu einem Modell?
  • Welche Faktoren sind vernachlässigbar, welche relevant?
  • Welche Beziehung besteht zwischen Modell und Realität?
  • Was kann man mit einem Modell anstellen?
    • Prognosen
    • Simulationen
    • Optimierung

Modell der Wärme

Wir benötigen drei Elemente:
  • Zweiter Hauptsatz der Thermodynamik respektive Wärmeleitungsgesetz
  • Wärmekapazität
  • Heizleistung

Wärmeleitungsgleichung

Modelle bilden nie alle Effekte der Realität korrekt ab. So zeigt etwa die Wärmeleitungsgleichung, d.h. die partielle Differentalgleichung $\frac{\partial T}{\partial t}=\frac{\partial^2T}{\partial x^2}$, eine unendliche (und damit unphysikalische) Ausbreitungsgeschwindigkeit: Eine Wärmequelle ist instantan im ganzen Raum spürbar. Die diskrete Gleichung zeigt dieses Phänomen übrigens nicht.

Programm

Ein kleines Mathematica-Programm ist hier beigefügt:

Wärmeleitung

Modellbildung

Ein zentrales Anliegen des Mathematik- und des Physikunterrichts ist die Modellbildung.

Besonders mächtige Modelle sind nach der Einführung der Infinitesimalrechnung möglich. So lange sollte man jedoch mit dem Thema Modellbildung nicht warten. Die folgende Idee bietet eine Möglichkeit, ohne den Ableitungsbegriff die Wärmeleitung zu behandeln, und dabei die Modellbildung mit mathematischen, physikalischen, numerischen und geologischen Überlegungen zu verbinden.

Eine gängige Methode der Modellbildung geht von "infinitesimalen" Betrachtungen an einem kleinen Intervall $\Delta x$ aus. Durch Grenzübergang $\Delta x\to 0$ gelangt man zu einer (gewöhlichen oder partiellen) Differentialgleichung. Bei der numerischen Analyse wird diese Differntialgleichung sodann wieder in der einen oder anderen Weise diskretisiert. Gelegentlich kann der Zwischenschritt aber übersprungen werden. Dadurch lässt sich direkt eine Differenzengleichung diskutieren und/oder implementieren:



Wir wollen dieses Vorgehen nun illustrieren und dabei die Diskussion der Wärmeleitung an den folgenden zwei miteinander verbundenen Fragen aufhängen:

Warum verbrennen wir uns nicht die Füsse an der Erdoberfläche?

Dies ist auf den ersten Blick eine seltsame Frage! Aber immerhin wird ein heisses Frühstücksei nach dem Abschrecken mit kaltem Wasser sehr schnell wieder von innen heraus heiss. Die Temperatur im Erdkern beträgt (je nach Quelle) rund 7000 K. Warum schmiltzt dann die Hitze aus dem Erdinnern im Lauf der Zeit die Erdkruste nicht komplett auf?


Wie alt ist die Welt?

Diese Frage stellte Lord Kelvin (William Thomson) 1862 im Zuge der Diskussion um die Evolutionstheorie. Darwins Gegner argumentierten, das durch die Bibel gegebene Alter der Erde von einigen Tausend Jahren sei viel zu gering, so dass die Evolution keine Zeit gehabt hätte überhaupt abzulaufen. Kelvin beabsichtigte durch eine physikalische Überlegung ein weit höheres Erdalter zu etablieren um so das Argument von Darwins Gegnern zu entkräften.

  • Kelvins Idee: Betrachte die Erde als abkühlenden Körper und berechne aus den Daten die Abkühldauer. Newtons Abkühlungsgesetz lässt sich zwar nicht direkt auf den Planeten Erde übertragen, aber wir werden weiter unten sehen, wie Kelvin im Prinzip vorgegangen ist.
  • Kelvins Resultat: 24 bis 400 Millionen Jahre.
  • Heute geschätztes Erdalter: 4.5 Milliarden Jahre.

Warum hat sich Lord Kelvin so verschätzt? Was Kelvin noch nicht wissen konnte: Im Erdinnern wird Wärme erzeugt durch

  • natürliche Radioaktivität (von Becquerel erst 1896 entdeckt)
  • Auskristallisieren des Erdkerns
  • Gezeitenkräfte (die resultierende Reibung erzeugt Wärme, wie beim Kneten eines Brotteigs)

Durch diese Effekte verlängert sich der Abkühlvorgang. Solange die erwähnten "inneren" Wärmequellen nicht versiegen wird die Erde auch nicht vollständig auskühlen sondern einem thermischen Gleichgewicht zustreben. Wir kommen darauf zurück.

Nun werden wir anhand einiger einfacher Überlegungen zu einem Modell der Wärme gelangen.

Modell der Wärme

Für das folgende ist es nicht nötig einen Begriff von kinetischer Wärmetheorie aufzubauen. Es genügen heuristische Beobachtungen, die durch Experimente illustriert und untermauert werden können. Wir stellen uns vor, dass Wärme eine Energieform ist, welche der Materie innewohnt und sich durch deren Temperatur manifestiert. Legt man sein heisses Frühstücksei in einen kleinen Topf mit kaltem Wasser, so stellt man fest, dass sich das Ei abkühlt und das Wasser leicht erwärmt, solange bis sich die Tempratur ausgeglichen hat. Der umgekehrte Vorgang, dass nämlich ein Ei dem umgebenden Wasser Wärme entzieht und spontan heiss wird, kommt nicht vor. Das ist der Inhalt des zweiten Hauptsatzes der Thermodynamik.

Zweiter Hauptsatz der Thermodynamik und Wärmeleitung

Eine Version dieses Satzes besagt:

Zweiter Hauptsatz der Wärmelehre
Wärme fliesst selbständig nur von einem Körper höherer zu einem Körper niedrigerer Temperatur.

Der zweite Hauptsatz zeigt also die Richung des Wärmeflusses an. 1822 formulierte Joseph Fourier eine quantitative Fassung der Wärmeleitung in seiner Théorie analytique de la chaleur:


fourier.jpg

Fourier argumentierte, dass die Wärmemenge $\Delta Q$, die in der Zeit $\Delta t$ von rechts nach links durch das Wandstück fliesst, proportional ist zu $\Delta t$, zur Fläche $A$ und zur Temperaturdifferenz $T_2-T_1$. So fliesst etwa durch ein doppelt so grosses Flächenstück doppelt so viel Wärme. Andererseits isoliert eine dickere Wand besser als eine dünne, das heisst $\Delta Q$ ist umgekehrt proportional zu Dicke $d$. In Formeln liest sich das so:

Wärmeleitungsgesetz
Die Wärmemenge $\Delta Q$, die in der Zeit $\Delta t$ von rechts nach links durch das Wandstück fliesst, ist

$\Delta Q=\lambda\, \Delta t\, A\, (T_2-T_1)\,\frac 1d$

Dabei bezeichnet $\lambda$ die Wärmeleitfähigkeit des Materials.

Wärmekapazität

Die Zufuhr von Wärme erhöht die Temperatur eines Körpers (sofern nicht gerade ein Phasenübergang stattfindet):

kapazitaet.jpg

Dies lässt sich zum Beispiel erreichen, indem man den Körper in Kontakt mit einem wärmeren Körper bringt, oder indem man die Wärme durch mechanische Reibung zuführt: Reibt man die Hände aneinander werden sie warm. Reibt man länger (leistet also mehr mechanische Arbeit), werden sie wärmer: Je mehr Wärme zufliesst, desto grösser wird die Temperaturerhöhung ausfallen. Andererseits braucht man bei doppelter Masse auch doppelt so viel Wärmeenergie für die selbe Temperaturerhöhung. Quantitativ lässt sich diese Aussage wie folgt fassen:

Wärmekapazität
Fliesst die Wämemenge $\Delta Q$ in eine Masse $m$ hinein, erhöht sich deren Temperatur um

$\Delta T = \frac 1c\frac{\Delta Q}{m}$

Dabei bezeichnet $c$ die spezifische Wärmekapazität des Materials.

Heizleistung

Die Heizleistung (etwa durch Radioaktivität im Erdinnern) ist definiert als die erzeugte Wärmemenge pro Masseneinheit und pro Zeiteinheit:

heitzleisung.jpg

Als Formel notiert ergibt sich:

Heizleistung
Im Zeitintervall $\Delta t$ werde in einem Massenstück $m$ die Wärmemenge $\Delta Q$ erzeugt. Dann ist die Heizleistung

$f=\frac{\Delta Q}{m\Delta t }$

Mit diesem Rüstzeug sind wir nun in der Lage, den zeitlichen Verlauf einer Temperaturverteilung zu modelliern.

Wärmeleitung im Stab

Frage: Wie entwickelt sich die Temperaturverteilung in einem Stab im Laufe der Zeit?

Für die Buchhaltung nehmen wir zunächst die Daten des Stabes auf:

  • Länge $L$
  • Querschnittsfläche $A$
  • Dichte $\rho$
  • Wärmeleitfähigkeit $\lambda$
  • Wärmekapazität $c$
  • Heizleistung $f$

Die Idee besteht darin, Messpunkte im Abstand $\Delta x=\frac Ln$ zu betrachten. An den einzelnen Messpunkten greifen wir die Temperatur $T_0(t), T_1(t),\ldots, T_n(t)$ zur Zeit $t$ ab:


stab1.jpg

Es ist naheliegend nicht nur den Ort, sondern auch die Zeit zu diskretisieren, d.h. wir interessieren uns nur noch für die Zeitpunkte $j\Delta t$. Auf diese Weise erhalten wir ein Gitter. Auf der horizontalen x-Achse nimmt der Stab das Intervall $[0,L]$ ein, nach oben tragen wir die Zeit $t$ ab:


gitter.jpg

Mit Tij bezeichnen wir dabei die Temperatur am Ort x = i Δx zur Zeit t = j Δt.

Betrachten wir im Detail den Wärmefluss am rot schraffierten Abschnitt des Stabes im Zeitintervall $[j\Delta t,(j+1)\Delta t]$ und berechnen den Wärmefluss mit Hilfe des Gesetzes von Fourier sowie die lokal erzeugte Wärme:


stabdetail.jpg

Von rechts hinein: $\Delta Q_{\rm{in}}\,= \lambda\, \Delta t\, A\,(T_{i+1j}-T_{ij})\frac 1{\Delta x}$
Nach links hinaus:   $\Delta Q_{\rm{out}}= \lambda\, \Delta t\, A\,(T_{ij}-T_{i-1j})\frac 1{\Delta x}$
Lokal erzeugt: $\Delta Q_{\rm{loc}}= f\,\Delta t\, A\,\Delta x\, \rho$

Das rot schraffierte Massenstück $m=A\,\Delta x\, \rho $ erlebt also im Zeitraum $\Delta t$ total die Wärmezunahme $\Delta Q_{\rm{in}} + \Delta Q_{\rm{loc}}-\Delta Q_{\rm{out}}$. Gemäss dem Gesetz der Wärmekapazität führt dieser Nettowärmezufluss zu einer entsprechenden Zunahme (oder Abnahme falls die Bilanz negativ ist) der Temperatur des Massenstücks:

\[ \Delta Q_{\rm{in}} + \Delta Q_{\rm{loc}}-\Delta Q_{\rm{out}} = A\,\Delta x \, \rho\,c\,(T_{ij+1}-T_{ij}) \]

Setzen wir die Terme linkerhand ein und formen um, so lautet diese Beziehung:

\[ \frac{\lambda}{\rho c}\frac{T_{i+1j}-2T_{ij} +T_{i-1j}}{\Delta x^2} +\frac fc = \frac{T_{ij+1}-T_{ij}}{\Delta t} \]


Dies ist die diskrete Wärmeleitungsgleichung in einer Raumdimension. Im Limes $\Delta x\to 0$, $\Delta t\to 0$ ergibt sich daraus die "richtige" Wärmeleitungsgleichung, eine partielle Differentialgleichung.

Durch Auflösen nach $T_{ij+1} $ ergibt sich ein numerisches Rechenschema, das sogenannte Richardson Verfahren:


richardson.jpg

Gibt man folgendes vor

  • Anfangstemperaturverteilung $T_{00}, T_{10}, \ldots, T_{n0}$
  • Randtemperatur links $T_{00},T_{01},\ldots$
  • Randtemperatur rechts $T_{n0},T_{n1},\ldots$

so lässt sich zeilenweise von unten beginnend die Temperatur in jedem Gitterpunkt berechnen:


richardsongitter.jpg

Das Resultat zeigt die Wärmeentwicklung bei konstanter Heizleistung im Stab im Laufe der Zeit:


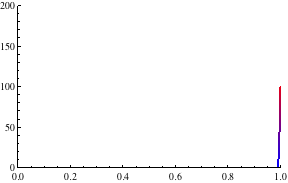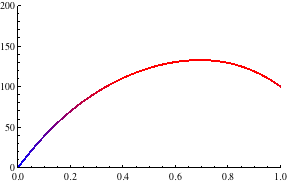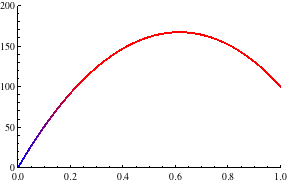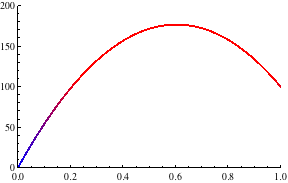
animation.gif

Als Beobachtung halten wir fest:

  • Die Lösung konvergiert gegen eine stationäre Verteilung
  • Die stationäre Verteilung scheint die Form einer Parabel zu haben (dies wird sich später bestätigen)
  • Spielt man im beigefügten Mathematica-Programm mit den Parametern, so zeigt sich, dass $\Delta t$ im Vergleich zu $\Delta x$ klein genug sein muss, damit das Richardson-Verfahren numerisch stabil ist. Es muss näich die Courant-Friedrich-Levy Bedingung gelten: $\frac{\lambda}{\rho c}\frac{\Delta t}{\Delta x^2}\le \frac 12$

Wärmeleitung in einer quadratischen Platte

Der Schritt von einem eindimensionalen Stab zu einer zweidimensionalen Platte ist einfach. Wir diskretisieren die Platte:

Randbedingung für $t>0$ Anfangsbedingungen
Am roten Rand: $T=100$
Am blauen Rand: $T=0$ 		$T=0$ zur Zeit $t=0$

Stellen wir die Wärmebilanz für das rot schraffierte Quadrat auf

quadratdetail.jpg

so erhalten wir

\[ \frac{\lambda}{\rho c} \frac{T_O(t)+T_N(t)+T_W(t)+T_S(t)-4T_Z(t)}{\Delta x^2}+\frac fc =\frac{T_Z(t+ \Delta t)- T_Z(t)}{\Delta t} \]

Dies ist die zweidimensionale Wärmeleitungsgleichung.

Für $f=0$ erhalten wir im stationären Fall:

\[ T_Z =\frac14(T_O+T_N+T_W+T_S) \]

Das heisst, im zentralen Punkt $Z$ ist die Temperatur das arithmetische Mittel der Nachbarpunkte in Norden, Süden, Osten und Westen. Diese Gleichung muss in jedem inneren Gitterpunkt $Z$ gelten. Man hat also ebensoviele Gleichungen wie Unbekannte.

Diskrete harmonische Funktionen
Die Temperatur in einem Gitterpunkt ist das arithmetische Mittel seiner Nachbarpunkte. Lösungen dieses linearen Systems heissen diskrete harmonische Funktionen.

Aus der Mittelwerteigenschaft folgt sofort:

Diskretes Maximumprinzip
Nimmt eine diskrete harmonische Funktione in einem inneren Punkt ihr Maximum an, so ist sie konstant.

Wendet man das diskrete Maximumprinzip auf die Differenz zweier Lösungen an, so bekommt man

Eindeutigkeit
Es existiert hochstens eine diskrete harmonische Funktion mit gegebenen Randwerten.

Und die lineare Algebra liefert daraus gratis hinzu:
Existenz
Zu beliebig vorgegebenen Randwerten existiert eine diskrete harmonische Funktion.

Für $n = 2$ und $n = 3$ kann man das entstehende Gleichungssystem noch von Hand lösen. Fur grosse $n$ ist selbst ein Computer mit Gauss-Elimination überfordert. Als Ausweg bieten sich zwei Methoden an:

  • Gauss-Seidel Iteration
  • Monte-Carlo Verfahren

Randbedingungen

Am Rand eines Gebietes können wir vorschreiben:

  • die Temperatur in jedem Punkt (Dirichlet-Randbedingung)
  • den Wärmefluss (Neumann-Randbedingung)

Die Neumann-Bedingung ist für unsere Ausgangsfrage wichtig, denn auf der Erdoberfläche finden wir die drei im Folgenden beschriebenen Effekte.

Sonneneinstrahlung

solar1.jpg

Solarkonstante $\Sigma = 1.36 \cdot 10^3 \frac{\rm{W}}{\rm{m}^2}$

Achtung: Die vom Querschnitt der Erde aufgefangene Leistung wird auf die ganze Kugeloberfläche verteilt:

solarred.jpg

Die effektive Solarkonstante reduziert sich somit auf einen Viertel des Wertes: $\bar\Sigma = \frac 14 1.36 \cdot 10^3 \frac{\rm{W}}{\rm{m}^2}$

Albedo-Effekt

albedo.jpg

Rund 31% der Sonneneinstrahlung wird wieder in den Weltraum zurückgeworfen. Die von der Sonne eingefangene Strahlungsleistung reduziert sich also auf den Wert $\bar\Sigma(1-a)$ mit $a = 0.31$.

Thermische Abstrahlung

kachelofen.jpg

Stefan-Bolzmann Strahlungsgesetz
Ein schwarzer Strahler der Temperatur $T$ strahlt von einem Flächenstück $A$ seiner Oberfläche die Leistung $P=\sigma AT^4$ ab. Dabei ist $\sigma= 5.67 \cdot 10^{-8}\frac{W}{\rm{m}^2\rm{K}^4}$ .

Bei einem realen Strahler reduziert sich die Emission um den Faktor $\varepsilon$. Nach dem Kirchhoffschen Strahlungsgesetz ist dieser Emissiongrad gleich dem Absorptionsgrad, für die Erde also $\varepsilon= 1 - a$.

Der eindimensionale Planet

planet1.jpg

Die eindimensionale Wärmeleitungsgleichung liefert:
\[ T_{i+1}-2T_i+T_{i-1}= -\frac{f\rho\,\Delta x^2}{\lambda} \]
Die zweite Differenzenfolge ist konstant, somit lautet die Lösung
\[ T_i=-\frac{f\rho\,\Delta x^2}{2\lambda} i^2+bi+c \]
Offenbar ist $c=T_0$ und aus Symmetriegründen ist $b=0$:
\[ T_i=-\frac{f\rho(i\Delta x)^2}{2\lambda}+T_0 \]
Setzen wir noch $x=i\Delta x$ so erhalten wir
\[ T(x)=T(0)-\frac{f\rho}{2\lambda} x^2 \]
Das ist sogar die exakte Lösung der dahinterstehenden Differentialgleichung.

Insbesondere gilt
  \begin{displaymath} T(0)-T(L)=\frac{f\rho}{2\lambda} L^2 \end{displaymath} (1)

Dies erklärt qualitativ unsere Ausgangsfrage!

Wir denken uns nun den Stab als Bohrkern durch die Erde mit entsprechenden Strahlungseffekten an den Stirnflächen: Die gesamte Heizleistung des Stabes ist gleich der an den beiden Stirnseiten des Stabes netto abgestrahlten Leistung. Also
  \begin{displaymath} f\rho L=(1-a)\sigma T(L)^4- \bar\Sigma(1-a) \end{displaymath} (2)

  • $L=$ mittlerer Erdradius $=6371\cdot 10^3$m
  • $\rho=$ mittlere Erddichte $=5.515\cdot 10^3\frac{\rm{kg}}{\rm{m}^3}$
  • $a=$ Albedowert der Erde $=0.31$
  • $\sigma = 5.670\cdot 10^{-8}\frac{\rm{W}}{\rm{m}^2\rm{K}^4}$
  • $\bar\Sigma =0.34\cdot 10^3\frac{\rm{W}}{\rm{m}^2}$
  • $\lambda=$ mittlere Wärmeleitfähigkeit Erde (Granit) $=2.8\frac{\rm{W}}{\rm{mK}}$
  • $T(L)=$ Mittlere Erdtemperatur $=288$K

Aus (2) erhält man $f=9.8\cdot 10^{-10} \frac{\rm{W}}{\rm{kg}}$

Aus (1) bekommt man dann $T(0)=3.9\cdot 10^7$K (unrealistisch!)

Der dreidimensionale Planet

Wir betrachten dünne Kugelschalen:

planet3.jpg

Fluss durch $K_{i-1}$ nach innen: $\lambda 4\pi(i-\frac12)^2\Delta x^2(T_i-T_{i-1})\frac1{\Delta x}$
Fluss durch $K_{i}$ nach innen: $\lambda 4\pi(i+\frac12)^2\Delta x^2(T_{i+1}-T_{i})\frac1{\Delta x}$
Heizleistung dazwischen: $f4\pi(i\Delta x)^2\Delta x\rho$

Die Bilanz ergibt:

\[ \frac{ (1+\frac1{2i})^2T_{i+1} - (2+\frac1{2i^2})T_i + (1-\frac1{2i})^2T_{i-1} }{ \Delta x^2 }= -\frac{f\rho}{\lambda} \]

Lassen wir quadratische Terme $\frac 1{i^2}$ weg, so ergibt sich

\[ (1+\frac1i)T_{i+1} -2 T_i +(1-\frac1i)T_{i-1}= -\frac{f\rho\Delta x^2}{\lambda} \]

Der Ansatz $T_i=a i^2+T_0$ liefert $a=-\frac{f\rho\Delta x^2}{6\lambda}$.

Somit
\[ T_i=-\frac{f\rho\Delta x^2}{6\lambda} i^2+T_0 \]

Setzen wir noch $x=i\Delta x$ so erhalten wir
  \begin{displaymath} T(x)=T_0-\frac{f\rho x^2}{6\lambda} \end{displaymath} (3)

Die Strahlenbilanz an der Oberfäche der Kugel mit Radius $R$
\[ f\frac43\pi R^3\rho = 4\pi R^2(\sigma T_R^4(1-a) -\bar\Sigma(1-a)) \]
ergibt die Randbedingung
  \begin{displaymath} \rho R f=3(1-a)(\sigma T(R)^4-\bar\Sigma) \end{displaymath} (4)

Aus (3) und (4) erhält man durch Elimination von $f$
\[ T(R)=T_0-\frac{R(1-a)(\sigma T(R)^4-\bar\Sigma)}{2\lambda} \]

Für eine Kerntemperatur $T(0)=7000$K und Erddaten wie zuvor erhält man eine Oberflächentemperatur $T(R)$ von etwas über $278$K und damit dann $f=3.6\cdot 10^{-11}\frac{\rm{W}}{\rm{kg}}$.

Fragen, die man nun diskutieren kann

  • Diskutiere Unterschiede zwischen Planet und Modell
% Konvektion, inhomogene Schichtung, Erdrotation, % Atmosphaere
  • Berechne in (3) $T'(R)$, also den
Temperaturgradienten an der Erdoberfläche (Erdwärmenutzung)
  • Berechne in (4) die Ableitung von $T(R)$ nach $a$,
also die Änderung der Gleichgewichtstemperatur bei Änderung der Albedo-Konstanten (Klimawandel)
  • Jupitermond Europa: Wie tief unter dem Eis liegt der (vermutete) Wasserozean?
% NASA: 50 km http://www.spiegel.de/wissenschaft/weltall/0,1518,535523,00.html

Page URL: https://wiki.math.ethz.ch/bin/view/PAM/Waermeleitung
31 Aug 2025
© 2025 Eidgenössische Technische Hochschule Zürich